Bootstrapping
即使採用了上一篇提及的所有技術，同態操作仍然總是會增加密文的誤差率（error rate），每次操作最多增加一個多項式因子。因此，到目前為止描述的方案只能同態地計算先驗有界深度（a-priori bounded depth）的電路；這樣的系統通常被稱為「部分同態（somewhat homomorphic）」或「分層（leveled）」。

Gentry 原始工作 [Gen09b, Gen09a] 中提出的一個精妙想法，稱為自舉（bootstrapping）或有時稱為刷新（refreshing），使得降低密文的誤差率成為可能，從而實現無限次數的同態計算（unbounded homomorphic computation）。假設有一個密文 c，它在秘密金鑰 s 下加密了某個（未知的）訊息 μ，其中 c 的誤差率太大而無法對其執行進一步的同態操作。自舉背後的思想是，在秘密金鑰 s 的一個低誤差加密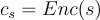

（該加密作為公開金鑰的一部分提供）上，同態地評估解密函數（homomorphically evaluate the decryption function）。更具體地說在密文 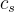上同態地評估函數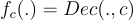
（請注意，要被刷新的密文 cc 被「硬編碼（hard-coded）」到函數 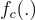中，而秘密金鑰則被視為函數的參數。）因為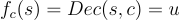

所以在 s 的一個加密，即 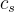上同態地評估 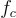會產生一個 μ 的加密。此外，只要 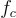的電路深度（circuit depth）和 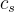的誤差率足夠小，輸出密文的誤差率將顯著小於輸入密文 c 的誤差率，如預期那樣。特別是，解密可以在 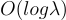深度內執行，因此 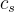只需具有某個 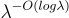的誤差率就足夠了。

因為自舉涉及對一個較為複雜的函數進行同態評估，所以它不是很高效，例如 [GH11b]。然而，自舉已經被深入研究並以各種方式改進[GH11a, BGV12], ，最終發展出基於環-LWE（ring-LWE）的方法，這些方法每個加密位元僅需多對數（polylogarithmic）時間 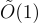即可運行 [GHS12a, AP13]，其中隱藏的 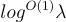因子並不過大。

通過指出以下一點來結束此討論：為了實現無限次數（unbounded）的同態操作，自舉需要一個秘密金鑰「在其自身下」的「循環（circular）」加密。揭示這樣一個加密是否是可證安全（provably secure）的（在標準假設下）尚屬未知，但也沒有已知的攻擊。因此，迄今為止，所有支持無限次數操作的全同態加密方案都需要一個關於秘密金鑰的循環安全性（circular security）的額外假設。

23.1 第三代全同態加密 (Third-Generation FHE)
2013年，Gentry、Sahai 和 Waters（以下簡稱 GSW）[GSW13] 提出了一個有趣的基於 LWE 的全同態加密方案，該方案具有一些獨特且有利的屬性。例如，同態乘法不需要任何金鑰交換步驟，並且該方案可以做成基於身份的。此外，如 [BV14, AP14] 所示，GSW 方案可以用於自舉，其錯誤率僅以一個小的 多項式 因子增長，而不是像上述系統那樣以擬多項式 (quasi-polynomial) 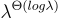因子增長。這使得基於 LWE 的無限制全同態加密僅需一個逆多項式 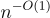的錯誤率（加上一個循環安全性假設）即可實現。接下來將詳細描述這些結果。

同態陷門 (Homomorphic trapdoors):
GSW 方案最簡單的表述方式是使用第 5.4.3 節中描述的基於小工具 (gadget-based) 的陷門。（這裡的表述經過了 [BGG+14, AP14, GVW15b] 的演變。）GSW 的核心在於以下對於 標籤 (tags) 和 陷門 的加法與乘法同態性。令 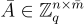是任意的，並且對於 i=1,2，令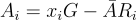

方程式 (23.1.4)
對於某個整數 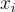和短的整數矩陣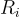

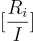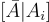換句話說 是矩陣 的一個帶有標籤 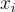或者更準確地說，是標籤 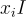的陷門。

應用方程式 (23.1.4)，很容易驗證：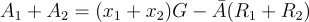

(23.1.5)

以及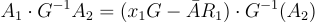



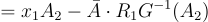
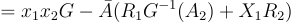
(23.1.6)

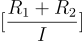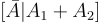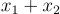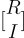換句話說 是矩陣 的一個帶有標籤 的陷門，而 是矩陣 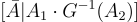的一個帶有標籤 的陷門。請注意，在後一種情況下，需要 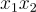是一個小的整數，以便獲得一個高品質的陷門。

同態乘法的一個非常重要的屬性是，所得到的陷門矩陣 R 的增長是非對稱的且擬加性的 (quasi-additive)：雖然 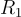，由於乘以 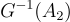而擴展了某個多項式因子，但 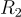項僅乘以

全同態加密 (Fully homomorphic encryption):
GSW 全同態加密方案的工作原理如下。與先前的系統一樣，公鑰是一個矩陣 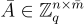，其列是帶有某個秘密 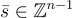的 LWE 樣本，即：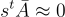

(23.1.7)

其中 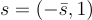是秘密金鑰。一個整數 x 的加密是一個矩陣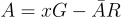

參考資料
[Gen09a] C. Gentry. A fully homomorphic encryption scheme. Ph.D. thesis, Stanford University, 2009. http ://crypto.stanford.edu/craig

[Gen10b] C. Gentry. Toward basing fully homomorphic encryption on worst-case hardness. In CRYPTO, pages 116–137. 2010.

[GH11b] C. Gentry and S. Halevi. Implementing Gentry’s fully-homomorphic encryption scheme. In EUROCRYPT, pages 129–148. 2011.

[GH11a] C. Gentry and S. Halevi. Fully homomorphic encryption without squashing using depth-3 arithmetic circuits. In FOCS, pages 107–109. 2011.

[BGV12] Z. Brakerski, C. Gentry, and V. Vaikuntanathan. (Leveled) fully homomorphic encryption without bootstrapping. TOCT, 6(3):13, 2014. Preliminary version in ITCS 2012.

[GHS12a] C. Gentry, S. Halevi, and N. P. Smart. Better bootstrapping in fully homomorphic encryption. In Public Key Cryptography, pages 1–16. 2012.

[AP13] J. Alperin-Sheriff and C. Peikert. Practical bootstrapping in quasilinear time. In CRYPTO, pages 1–20. 2013.

[GSW13] C. Gentry, A. Sahai, and B. Waters. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In CRYPTO, pages 75–92. 2013.

[BV14] Z. Brakerski and V. Vaikuntanathan. Lattice-based FHE as secure as PKE. In ITCS, pages 1–12. 2014.

[AP14] J. Alperin-Sheriff and C. Peikert. Faster bootstrapping with polynomial error. In CRYPTO, pages 297–314. 2014.

[BGG+14] D. Boneh, C. Gentry, S. Gorbunov, S. Halevi, V. Nikolaenko, G. Segev, V. Vaikuntanathan, and D. Vinayagamurthy. Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In EUROCRYPT, pages 533–556. 2014.

[GVW15b] S. Gorbunov, V. Vaikuntanathan, and D. Wichs. Leveled fully homomorphic signatures from standard lattices. In STOC, pages 469–477. 2015.